Khám Phá Nghệ Thuật Tìm Điểm Cực Tiểu Của Đồ Thị Hàm Số

Giới Thiệu: Ý Nghĩa Của Điểm Cực Tiểu Trong Toán Học

Trong thế giới toán học, việc tìm điểm cực tiểu của một hàm số là một kỹ năng quan trọng, được ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, kinh tế, và khoa học máy tính. Điểm cực tiểu là điểm thấp nhất của một đồ thị hàm số, nơi giá trị của hàm đạt mức tối thiểu.

Ý Nghĩa Của Việc Tìm Điểm Cực Tiểu

Việc xác định điểm cực tiểu giúp chúng ta:

Hiểu sâu hơn về hành vi của hàm số
Giải quyết các bài toán tối ưu hóa
Dự đoán xu hướng trong các mô hình khoa học

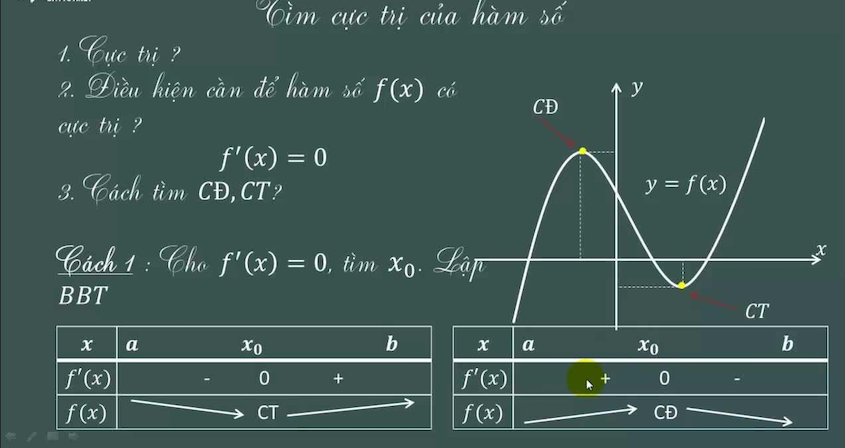
Các Phương Pháp Tìm Điểm Cực Tiểu

1. Phương Pháp Đạo Hàm

Bước 1: Tính Đạo Hàm

Để tìm điểm cực tiểu, chúng ta sử dụng phương pháp đạo hàm. Các bước cụ thể như sau:

Tìm đạo hàm của hàm số f(x)
Giải phương trình f'(x) = 0 để tìm các điểm nghi ngờ

Bước 2: Kiểm Tra Tính Chất Điểm Cực Tiểu

Sử dụng phép thử đạo hàm bậc hai (f”(x))
Nếu f”(x) > 0 tại điểm x, đó là điểm cực tiểu
Nếu f”(x) < 0 tại điểm x, đó là điểm cực đại

Xem thêm Khám Phá Bí Ẩn Hàm Số Đồng Biến Trên Không Gian R: Một Hành Trình Toán Học

2. Ví Dụ Minh Họa

Ví Dụ 1: Hàm Bậc Hai

Xét hàm số f(x) = x² + 4x + 4

Đạo hàm: f'(x) = 2x + 4
Giải f'(x) = 0: 2x + 4 = 0
x = -2 (điểm nghi ngờ)
Kiểm tra f”(x) = 2 > 0, nên (-2, 0) là điểm cực tiểu

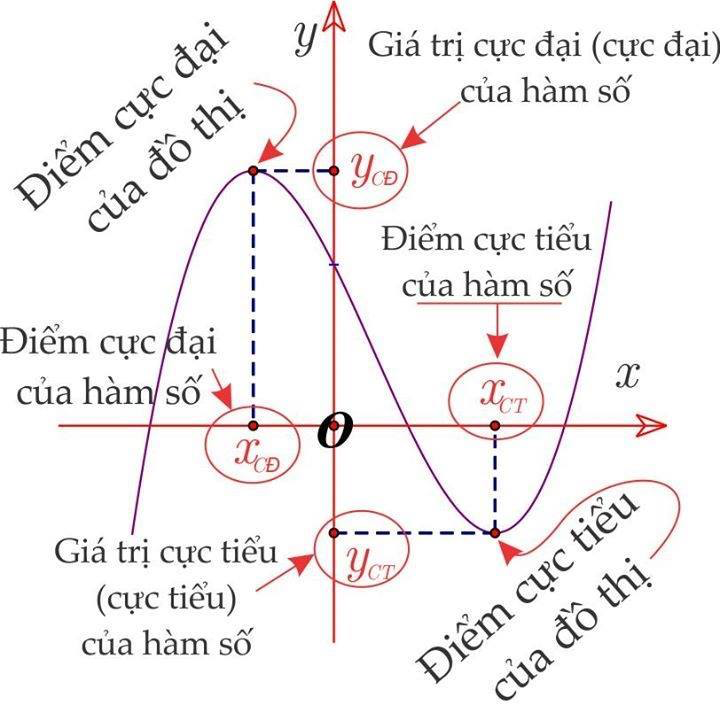
Các Phương Pháp Tìm Điểm Cực Tiểu Của Đồ Thị Hàm Số chi tiết

Ví Dụ 2: Hàm Lượng Giác

Xét hàm số f(x) = cos(x)

Đạo hàm: f'(x) = -sin(x)
Điểm f'(x) = 0 là khi sin(x) = 0
x = nπ (với n là số nguyên)
Kiểm tra các giá trị để xác định điểm cực tiểu

3. Phương Pháp Số Học

Phương Pháp Gradient Descent

Thuật toán lặp để tìm điểm cực tiểu
Áp dụng nhiều trong học máy và tối ưu hóa

Xem thêm Khám Phá Bí Ẩn Của Phương Trình Tiếp Tuyến: Hành Trình Toán Học Kỳ Thú

Ứng Dụng Thực Tế

Trong Kinh Tế

Tìm điểm chi phí tối thiểu
Xác định lợi nhuận tối ưu

Trong Vật Lý

Tính năng lượng tối thiểu của hệ
Phân tích chuyển động vật lý

Ứng Dụng Tìm Điểm Cực Tiểu Của Đồ Thị Hàm Số trong Xác định lợi nhuận tối ưu

Những Lưu Ý Quan Trọng

Hạn Chế Của Phương Pháp

Không phải hàm số nào cũng có điểm cực tiểu
Cần kiểm tra kỹ các điều kiện toán học

Kỹ Năng Cần Thiết

Kiến thức về đạo hàm
Khả năng phân tích logic
Tư duy toán học linh hoạt

Kết Luận: Sức Hấp Dẫn Của Toán Học

Việc tìm điểm cực tiểu không chỉ là một bài toán thuần túy, mà còn là một nghệ thuật khám phá bản chất sâu sắc của các hàm số. Nó đòi hỏi sự kết hợp giữa logic toán học và trí tưởng tượng sáng tạo.